Uniform Circular Motion describes the movement of an object traveling a circular path with constant speed. The one-dimensional projection of this motion can be described as simple harmonic motion.
Uniform Circular Motion describes the movement of an object traveling a circular path with constant speed. The one-dimensional projection of this motion can be described as simple harmonic motion.
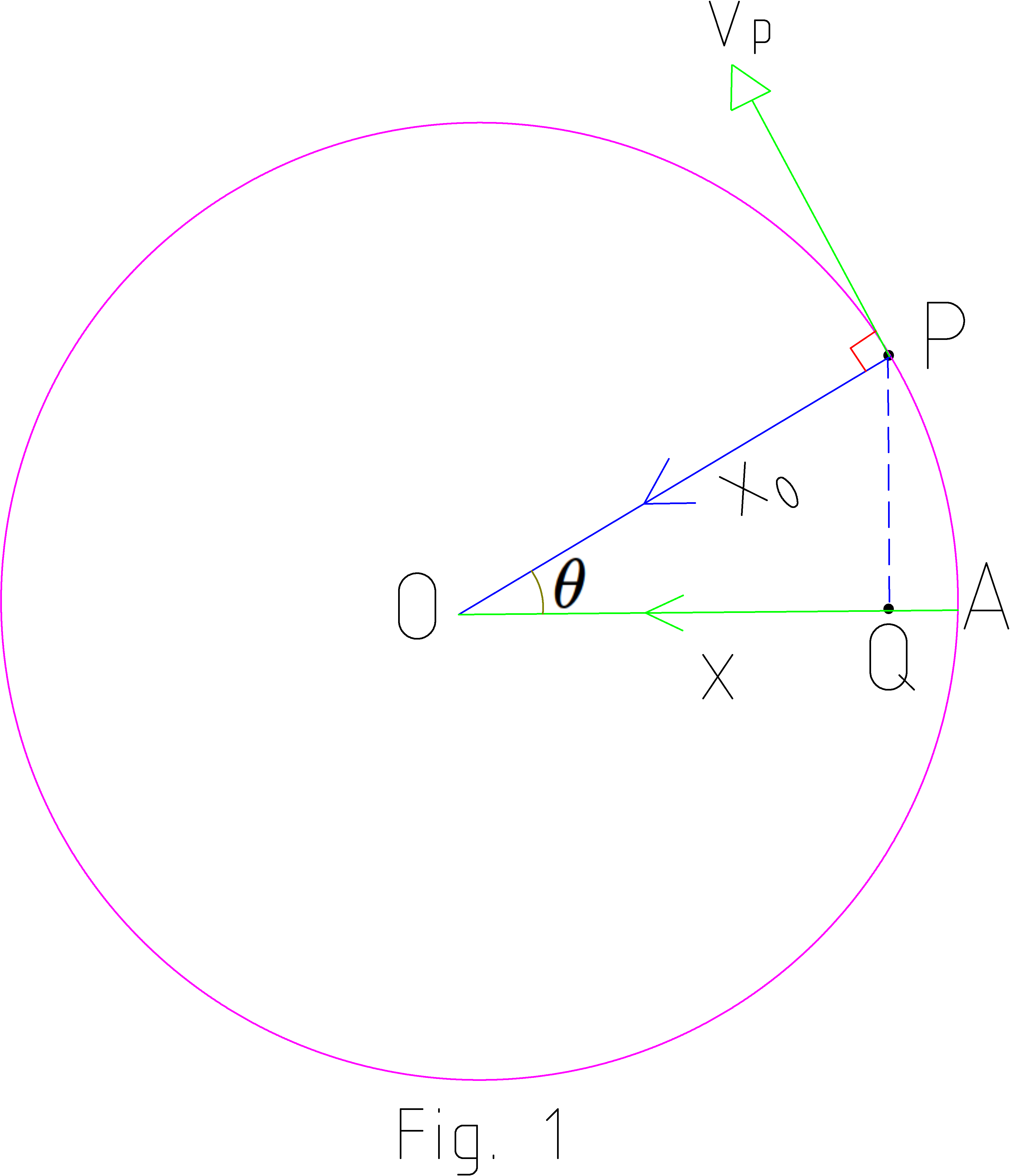
A point P moving on a circular path with a constant angular velocity ω is undergoing uniform circular motion. Its projection Q on the x-axis undergoes simple harmonic motion.
Let us consider point p, at time t=0 it is at A. It starts moving in circular path with angular velocity ω. After time t it will go to point p making angle ∠ AOP=θ =ωt at centre. Its projection will move to point Q. The displacement x of Q at instant will be $$ x=OQ=OP cos\angle AOP $$ $$ x= x_{0}cos\theta $$ $$ x=x_{0}cos\omega t $$ $$ $$ This is the instantaneous displacement of Q.
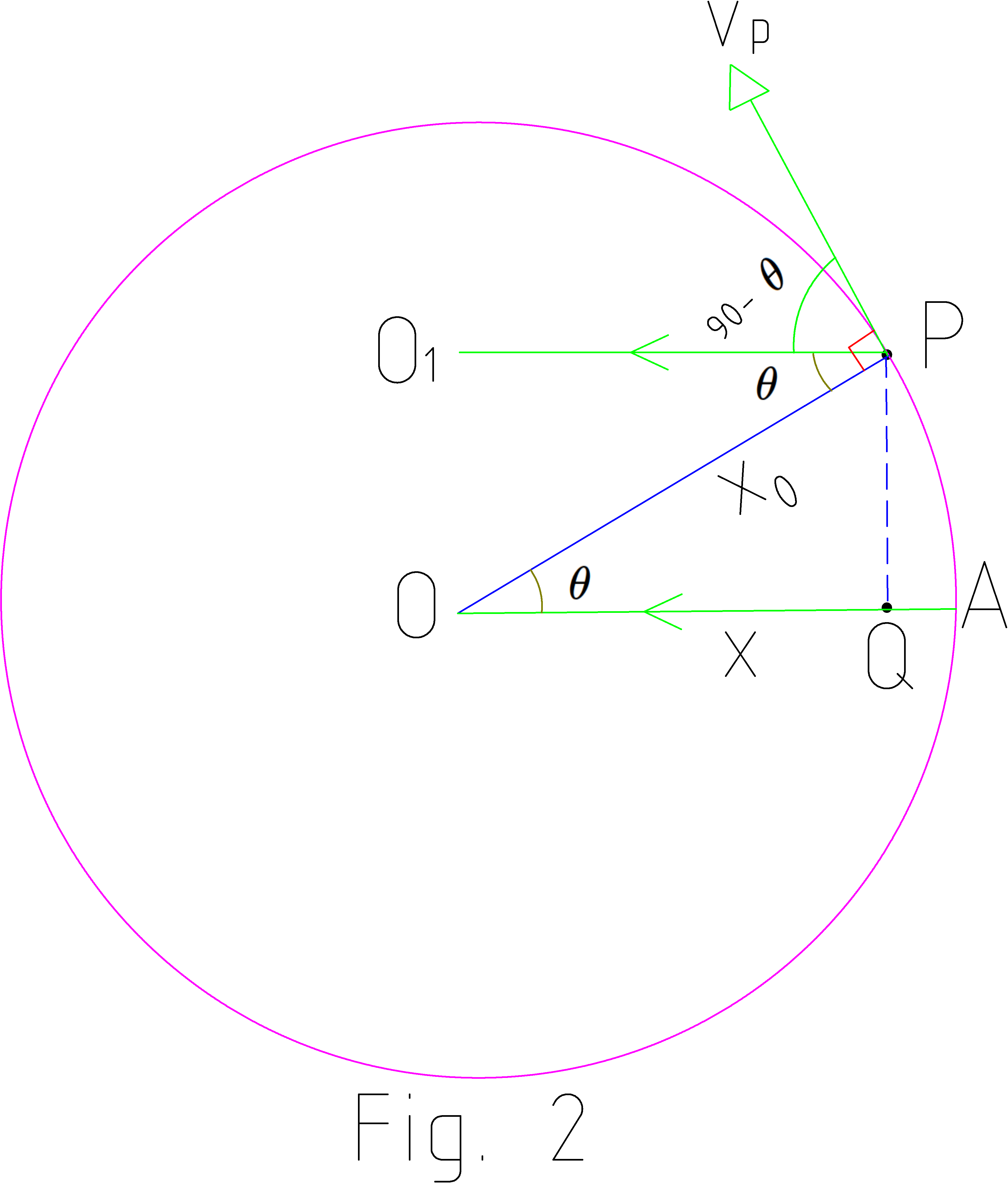The velocity of point P at instant t will be directed along the tangent to the circle at point P and its magnitude will be
$$ v_{p}=x_{0}\omega \; \; \; \; \; \because v=r\omega
\;\;\;\; \cdot \cdot\cdot\cdot (1)$$
As the motion of Q on the diameter is due to the motion of P on the circle, the velocity v of point Q is actually the component of the velocity Vp in a direction parallel to diameter (AO || PO1). So
$$
v=v_{p}cos(90-\theta) \; \; \; \; \; \because cos(90-\theta) = sin\theta $$ $$
v=v_{p} sin\theta $$ $$
= x_{0}\omega sin\theta \;\;\;\; \cdot \cdot\cdot\cdot (2)$$ $$
But \; \; \; sin^2\theta + cos^2\theta = 1 $$ $$
sin\theta = \sqrt{1-cos^2\theta} $$ so eq(2) becomes
$$ v = x_0 \omega \sqrt{1-cos^2\theta} $$ From figure 1 $$
cos\theta = \frac{x}{x_{0}} $$ $$
putting \; in \; above \; equation $$ $$
v = x_0 \omega \sqrt{1-\frac{x^2}{x^2_{0}}} $$ $$
v=x_{0}\omega \sqrt{\frac{x^2_{0}-x^2}{x^2_{0}}} $$ $$
v=x_{0}\omega \sqrt{\frac{x^2_{0}-x^2}{x^2_{0}}} $$ $$
v=\frac{x_{0}\omega}{x_{0}}\sqrt{x^2_{0}-x^2} $$ $$
= \omega \sqrt{x^2_{0}-x^2} $$ $$
when \; x=0 , \; velocity \; is \; maximum $$
$$
v_{max}= \omega {x_{0}}\sqrt{x^2_{0}} $$
$$
when \; x=x_{0} $$
$$
v=0 $$
If ac is the centripetal acceleration of body directed towards the mean position O.
We can resolve the centripetal acceleration into its x and y components.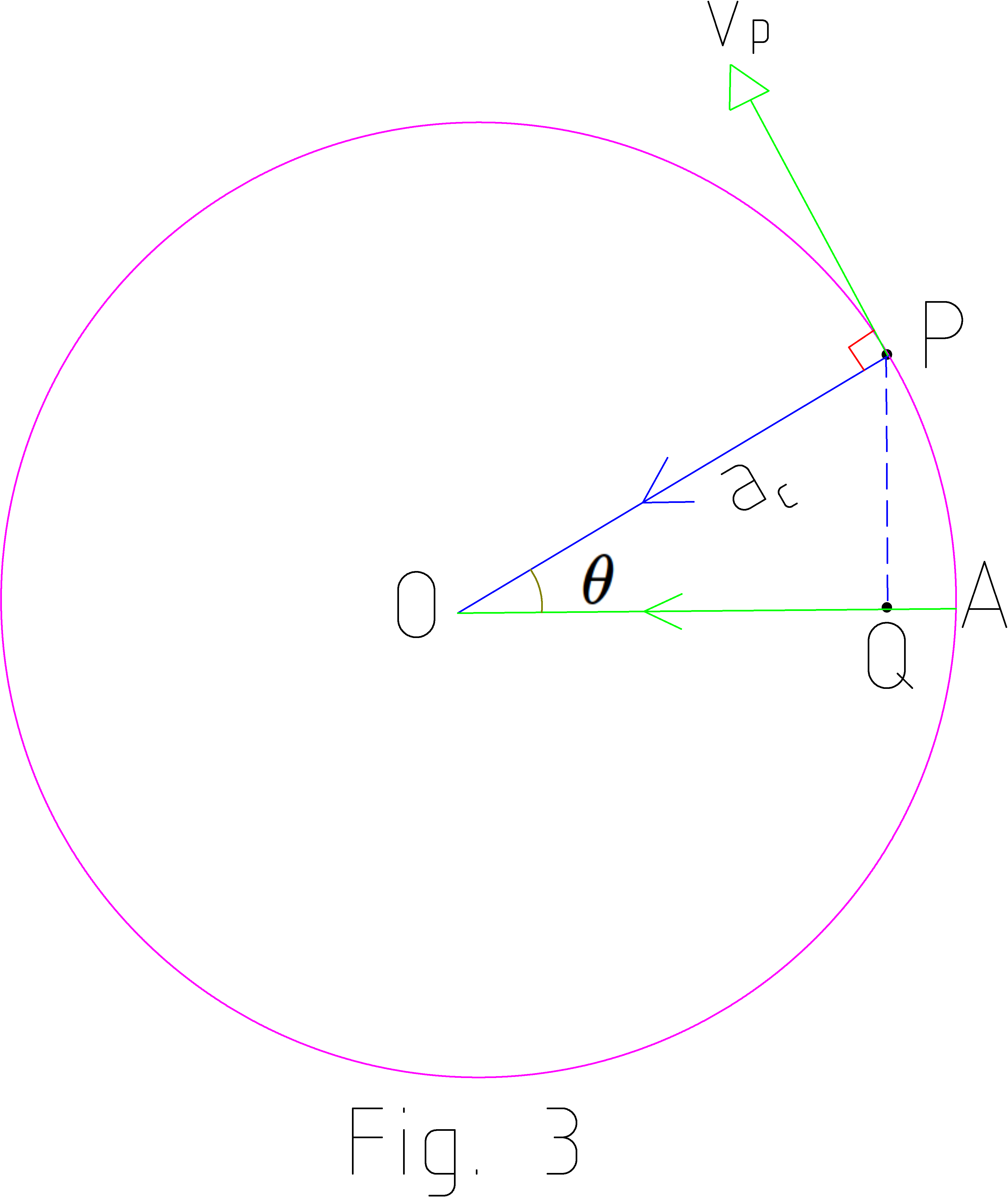
Its component along the diameter is
$$ a_{x}=a_{c} cos\theta \;\;\;........\;\;\ (2)$$
As we know
$$a_{c}=\frac{v^2}{r} $$
as
$$v=r\omega $$
so
$$a_{c}=\frac{(r\omega)^2}{r} $$
$$a_{c}=r\omega^2$$
putting the value in eq 2
$$a_{x}=r\omega^2 (cos\theta)$$
From fig 1, we see that △ OQP is a rigth angle triangle and r=x0 . So
$$ \frac{x}{r}=cos\theta $$
$$ x=rcos\theta$$
puting in eq 2
$$a_{x}=r\omega^2 (\frac{x}{r}) = \omega^2 x $$
As ax is directed towards the mean position so we take its sign negative and above equation becomes
$$ a_{x}=\omega^2 (-x)$$
for ω = constant
$$ a_{x}= -constant \times x$$
or
$$ a_{x} \propto -x$$
This equation is the equation of Simple Harmonic Motion